新久郎の言葉を相手にせず、少年は今度は三角形を描き始めた。
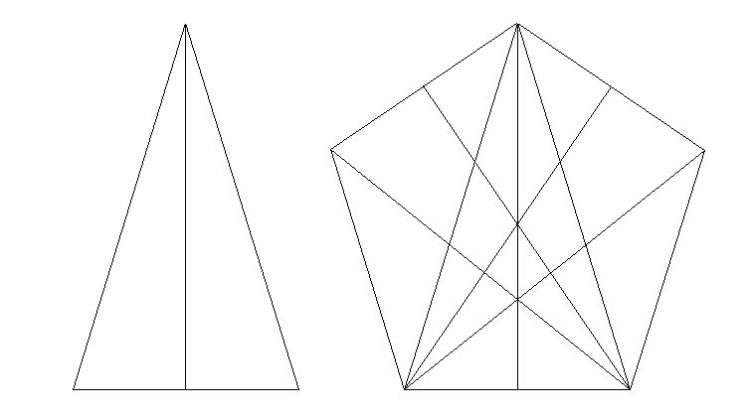
　まずは底辺を横一文字に描き、その中点を取る。
　垂直に線を描き、斜めの辺を描いて二等辺三角形にするのだが、少年は底辺の半分を指で測り、その三つ分と少しの長さだけ合うところに印を付けて線をつないだ。
　新久郎もしゃがみ込んで少年の顔をのぞき込む。
「今度は何をしておるのだ？」
「じゃま」
　ハエでも追い払うように扱われてしまうが、彼は怒らず場所を譲った。
　少年はその二等辺三角形の向きを変え、辺がそろうように並べて書き加えていく。
　すると、またきれいな正五角形ができあがるのだった。
「ほう、まるで魔法のようだな。これもおぬしが考えたものか？」
　少年はやはり答えない。
「五角形が好きか？」
　少年はコクンとうなずく。
「私は幾何が苦手でな。先日も半径が七の円の面積を問われて居残りしたものさ」
「百五十三と八分六厘」
「なんと！」
　まるで歳でも聞かれたかのように少年が即答するもので、新久郎は思わず尻餅をついてしまった。
「なぜだ？　ソロバンもないのにどうやって計算した？」
　少年はまた口を固く結んでうつむいてしまった。
「なあ、おぬし、この問題が解けるか？」
　新久郎は起き直ると、尻もはたかず、藩校で出された宿題を取り出して読み上げた。
『元服してまもない太郎の歳を五つに分けて三つ分を取れば次郎の歳となり、次郎の歳を三つに分けて二つ分を取れば三郎の歳となる。兄弟各々の齢を問うものなり』
「十五、九、六」
「本当か……」と、新久郎は十五を五で分け、三倍し、それを三つに分けて二倍してみた。「ほう、真だな。どうして分かる？」
　少年はうつむいたままつぶやく。
「三が一緒だから、五と三と二をそれぞれかける。それに、元服に近い歳で五で割れる数は十五しかないから」
　今までで一番長くしゃべった。
　その声は極楽浄土に鳴く鳥のさえずりのように新久郎の耳に残った。
　と、ここで新久郎はふと思いついたことを尋ねてみた。
「なあ、この問いは十五と九と六の倍数であれば他にも答えが見つかるな。三十、十八、十二でも、四十五と二十七と十八。それと……」
　その後を少年が引き継いだ。
「もし還暦であれば六十と三十六と二十四だけど、兄弟と言うには歳が離れすぎる」
「おお、なるほど、そうだな。まるで親子のようになってしまうか。『元服して間もない』とはそういうことか。これは気がつかんかった」
　ほんの少し少年の頬に笑みが浮かんだように思えた。